DSA Selection Sort Time Complexity
See this page for a general explanation of what time complexity is.
Selection Sort Time Complexity
The Selection Sort algorithm goes through all elements in an array, finds the lowest value, and moves it to the front of the array, and does this over and over until the array is sorted.
Selection Sort goes through an array of \(n\) values \(n-1\) times. This is because when the algorithm has sorted all values except the last, the last value must also be in its correct place.
The first time the algorithm runs through the array, every value is compared to find out which one is the lowest.
The second time the algorithm runs through the array, every value except the first value is compared to find out which is the lowest.
And in this way the unsorted part of the array becomes shorter and shorter until the sorting is done. So on average, \(\frac{n}{2}\) elements are considered when the algorithm goes through the array finding the lowest value and moving it to the front of the array.
In addition to all the compares needed, the number of swap considerings needed is \(n -1 \).
We can start calculating the number of operations for the Selection Sort algorithm:
\[ \begin{equation} \begin{aligned} Operations {} & = (n-1)\cdot \frac{n}{2} + (n - 1) \\ & = \frac{n^2}{2} - \frac{n}{2} + (n - 1) \\ & = \frac{n^2}{2} + \frac{n}{2} \end{aligned} \end{equation} \]
When looking at the run time for algorithms, we look at very large data sets, meaning \(n\) is a very big number. And for a very big number \(n\), the term \(\frac{n^2}{2}\) becomes so much bigger than the term \(\frac{n}{2}\) that we can approximate by simply removing that second term \(\frac{n}{2}\).
\[Operations = \frac{n^2}{2} + \frac{n}{2} \approx \frac{n^2}{2} = \frac{1}{2} \cdot n^2 \]
Using Big O notation to describe the time complexity for the Selection Sort algorithm, we get:
\[ O( \frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]
And time complexity for the Selection Sort algorithm can be displayed in a graph like this:
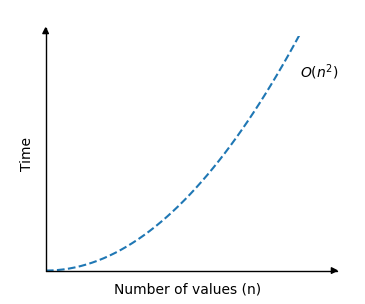
As you can see, the run time is the same as for Bubble Sort: The run time increases really fast when the size of the array is increased.
Selection Sort Simulation
Run the simulation for different number of values in an array, and see how the number of operations Selection Sort needs on an array of \(n\) elements is \(O(n^2)\):
{{ this.userX }}
Operations: {{ operations }}
The most significant difference from Bubble sort that we can notice in this simulation is that best and worst case is actually almost the same for Selection Sort (\(O(n^2)\)), but for Bubble Sort the best case runtime is only \(O(n)\).
The difference in best and worst case for Selection Sort is mainly the number of swaps. In the best case scenario Selection Sort does not have to swap any of the values because the array is already sorted. And in the worst case scenario, where the array already sorted, but in the wrong order, so Selection Sort must do as many swaps as there are values in the array.

