A Simple Algorithm
Fibonacci Numbers
The Fibonacci numbers are very useful for introducing algorithms, so before we continue, here is a short introduction to Fibonacci numbers.
The Fibonacci numbers are named after a 13th century Italian mathematician known as Fibonacci.
The two first Fibonacci numbers are 0 and 1, and the next Fibonacci number is always the sum of the two previous numbers, so we get 0, 1, 1, 2, 3, 5, 8, 13, 21, ...
Create fibonacci numbers.
{{ msgDone }}This tutorial will use loops and recursion a lot. So before we continue, let's implement three different versions of the algorithm to create Fibonacci numbers, just to see the difference between programming with loops and programming with recursion in a simple way.
The Fibonacci Number Algorithm
To generate a Fibonacci number, all we need to do is to add the two previous Fibonacci numbers.
The Fibonacci numbers is a good way of demonstrating what an algorithm is. We know the principle of how to find the next number, so we can write an algorithm to create as many Fibonacci numbers as possible.
Below is the algorithm to create the 20 first Fibonacci numbers.
How it works:
- Start with the two first Fibonacci numbers 0 and 1.
- Add the two previous numbers together to create a new Fibonacci number.
- Update the value of the two previous numbers.
- Do point a and b above 18 times.
Loops vs Recursion
To show the difference between loops and recursion, we will implement solutions to find Fibonacci numbers in three different ways:
- An implementation of the Fibonacci algorithm above using a
forloop. - An implementation of the Fibonacci algorithm above using recursion.
- Finding the \(n\)th Fibonacci number using recursion.
1. Implementation Using a For Loop
It can be a good idea to list what the code must contain or do before programming it:
- Two variables to hold the previous two Fibonacci numbers
- A for loop that runs 18 times
- Create new Fibonacci numbers by adding the two previous ones
- Print the new Fibonacci number
- Update the variables that hold the previous two fibonacci numbers
Using the list above, it is easier to write the program:
Example
prev2 = 0
prev1 = 1
print(prev2)
print(prev1)
for fibo in range(18):
newFibo = prev1 + prev2
print(newFibo)
prev2 = prev1
prev1 = newFibo2. Implementation Using Recursion
Recursion is when a function calls itself.
To implement the Fibonacci algorithm we need most of the same things as in the code example above, but we need to replace the for loop with recursion.
To replace the for loop with recursion, we need to encapsulate much of the code in a function, and we need the function to call itself to create a new Fibonacci number as long as the produced number of Fibonacci numbers is below, or equal to, 19.
Our code looks like this:
Example
print(0)
print(1)
count = 2
def fibonacci(prev1, prev2):
global count
if count <= 19:
newFibo = prev1 + prev2
print(newFibo)
prev2 = prev1
prev1 = newFibo
count += 1
fibonacci(prev1, prev2)
else:
return
fibonacci(1,0)3. Finding The \(n\)th Fibonacci Number Using Recursion
To find the \(n\)th Fibonacci number we can write code based on the mathematic formula for Fibonacci number \(n\):
\[F(n) = F(n-1) + F(n-2) \]
This just means that for example the 10th Fibonacci number is the sum of the 9th and 8th Fibonacci numbers.
Note: This formula uses a 0-based index. This means that to generate the 20th Fibonacci number, we must write \(F(19)\).
When using this concept with recursion, we can let the function call itself as long as \(n\) is less than, or equal to, 1. If \(n \le 1\) it means that the code execution has reached one of the first two Fibonacci numbers 1 or 0.
The code looks like this:
Example
def F(n):
if n <= 1:
return n
else:
return F(n - 1) + F(n - 2)
print(F(19))Notice that this recursive method calls itself two times, not just one. This makes a huge difference in how the program will actually run on our computer. The number of calculations will explode when we increase the number of the Fibonacci number we want. To be more precise, the number of function calls will double every time we increase the Fibonacci number we want by one.
Just take a look at the number of function calls for \(F(5)\):
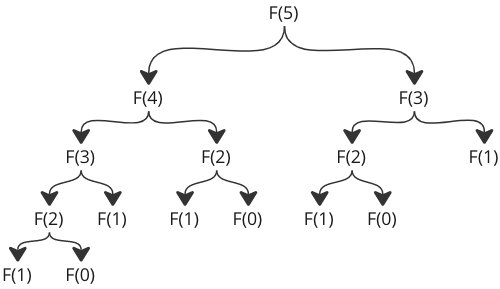
To better understand the code, here is how the recursive function calls return values so that \(F(5)\) returns the correct value in the end:
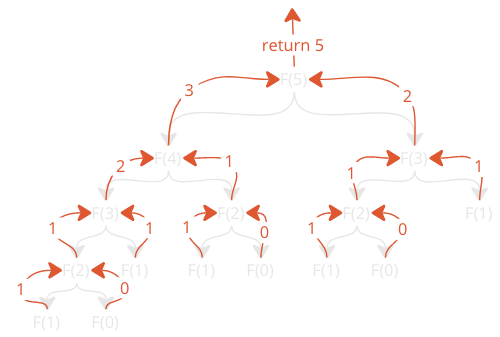
There are two important things to notice here: The amount of function calls, and the amount of times the function is called with the same arguments.
So even though the code is fascinating and shows how recursion work, the actual code execution is too slow and ineffective to use for creating large Fibonacci numbers.
Summary
Before we continue, let's look at what we have seen so far:
- An algorithm can be implemented in different ways and in different programming languages.
- Recursion and loops are two different programming techniques that can be used to implement algorithms.
It is time to move on to the first data structure we will look at, the array.
Click the "Next" button to continue.

